小中学校で、算数や数学に苦手意識を持たせないために。もっと算数の根本的な考え方を理解して、未就学児のうちに数学的思考力をつけさせるのが狙いの連載です。周囲の大人が注目するべき、子どもの動きとそのフィードバック方法、その後のアプローチの仕方を毎回3ステップでお伝えしています。

子どもが自ら、【同じ】を発見し、その【理由】探しができるようにしています。

最終回は変化の【理由】の気づきです。

連載の第7回では、「過去や未来を予測し、問題解決ができる」という「関数の考え」の特性に触れました。今回取り上げたい「関数の考え」の特性は「概念を作る」です。

「幸せって何？」「美味しいって何？」「楽しいって何だろう？」……。「なぜなに期（質問期）」という時期を中心に、子どもはありとあらゆる質問を周囲に浴びせかけます。

実はここで「わからないものを既にわかっているものに関係付けて説明する」という「関数の考え」が活躍するのです。

前回の連載で説明した4段階は「概念を作る」というステップでもあるのです。ちょっと難しいかもしれないですが、ぜひ、小さい子どもの頃からこれを体験して欲しいのです。

具体的に説明していきますね。

文部科学省は、これからは問題解決能力だけではなく問題発見能力を伸ばすことも大事だ、としています。

そもそも幼児期には、子どもは皆、常に問いを発していますよね、問いだらけです。

でも……「うるさいわね、電車の中では静かにしなさい」って親に言われたり、「授業中は、先生の話を静かに聞くこと！」なんて言われたりして、どんどん萎縮してしまいがちに。学校では「ここ、わからないんですけど」と声をあげにくい状況になっている子もまだまだ多いかもしれません。「バカなこと言わないように」「質問ばかりする子は鬱陶しい」など、恥の文化なんて背景もありますが、今後は日本もどんどん黙っている方が悪い状況になる社会になりつつあります。積極的に質問し、わからないことは声をあげて主張する必要があるのです。

そこで、まず、子どもが自ら問うこと自体を「いい質問だね」「いいことに気が付いたね」と認め、褒めてあげましょう。

そして、子どもがなぜ？を投げかけてきたら、解答をすぐに与えることよりも、むしろ「ママ（パパ）もわからないよ、なぜなんだろうね」と言ってあげることが大事です。

「わからない」を言うことが「わかること」のはじまりだからです。

「知らないということを知っている」のは、ソクラテスの「無知の知」ですが、この「わからない」から問いを見出すのが、「関数の考え」のはじまりだと思っています。なぜなら、これが概念規定の一つの方法だからです。

例えば子どもが「速いって何？」と聞いてきた時には、必ず対立概念があります。対立概念があるということは変数であることなのです。新幹線と在来線を見比べて「ママ、この電車のろいよ、こっちが速い！」と言っているのかもしれません。何かに比べて速いと感じる、つまり相対性なのです。となると、いよいよ「関数の考え」が登場します。

イソップの寓話に「ウサギとカメ」の有名な話があります。さて、結局ウサギとカメはどっちがはやかったのでしょうか……？

小学校で習う算数の定義でいうと、カメです。

ある一定の距離を短い時間で行った方が速いとされるからですが、子どもたちも運動会やプールで体験済みなので納得する答えですね。速さは、時間と距離で決めましょう、というのが小学校の算数です。

ところが、物理学では違う捉え方もします。瞬間の平均変化率、つまり微分で決めると、ウサギの方が早いのです。

というように、速さひとつとっても、何に依存させるかによって概念は変わってくるのです。それを味わってほしいのです。

子「楽しいって何？」
大人「楽しいの反対はなあに？」
子「つまんない、かな？」
大人「楽しいとつまんないって何だろうね？」
子「笑いかな？笑いがたくさんあるといいのかも。笑の数がたくさんあれば、毎日楽しいね！」

これは「関数の考え」ですよね。

「何によって決まるんだろう」と一緒に考えて、そこに正解を出さなくても「そうだね、それかもしれないね」でいいと思います。

他にも「明るいね」「こっちは暗いね」「時間が経つと変わっていくね」「明るさって何で決まるんだろうね」「電気？太陽かな？」「曇りの時はちょっと暗いね？」「天気で決まる？」「そうかもしれないね」そういう会話を楽しんでみてください。

家庭菜園や近所の草花で、昨日は葉っぱが2枚だったのに朝には4枚に増えていた、花が昨日は1輪しか咲いていなかったのに今日は3輪咲いていた、など、昨日とは違う数のものを親子で一緒に発見してみましょう。

数字が読めるようになったら、家にかけてある日めくりカレンダーや、街の中の気温を表す温度計、住所を表す番地など、あるいは車の走行距離、水道のメーターなど、身の回りや街の中にある数も意識してその変化に目を留めてみましょう。時計もわかりやすいかもしれませんね。

トイレトレーニングや、歯磨きができた日に、シールを貼って表やグラフを作っているご家庭も多いかもしれません。これ、何によってできるようになったかを考えると面白いですね。

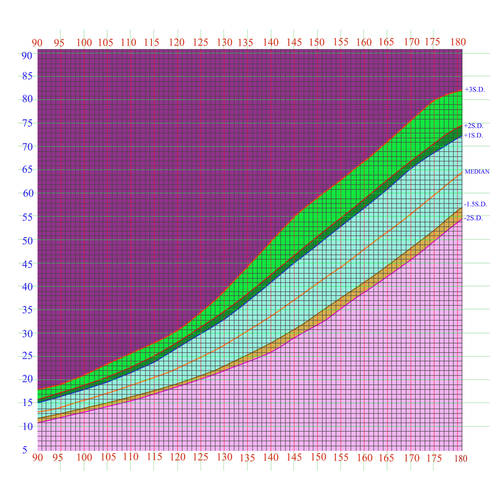
成長曲線を見て、体重、身長も何によって増えているのかな？と考えてみるのも良いでしょう。
放物線を見せて、だんだん増えてるね、だんだん減ってるね、なんて子どもが言えたら最高ですね。

何かの機会に目にする表やグラフを見てそんな会話をしてみてください。

グラフと表は、必ずYとXが出てきて、二つが伴って変わる量が出てくるのです。

小学校1、2年で教える表はまだ一元的です。例えば1年生ですぐに「誕生日調べ」をします。4月生まれが何人、5月生まれが何人とするのですね。月によって人数が違うことには皆気付きます。
これが4年生ともなると、曜日と怪我の数など、何かと何かを表にしていくようになります。

さらに、50％、2割、1/2などの関係数に少しずつ触れてほしいです。これらは依存関係の表現です。スーパーなどで買物する時にも表示書きに注意して、親子で会話してみると良いかもしれませんね。

陶冶（とうや）という言葉には「陶器を作ること」という意味の他に、人間の性質や能力を育てること、人間を形作っていくこと、というような意味があります。

教育用語として、ドイツ語のbildung（英語：building）を翻訳して当てられた言葉ですが、そういう何かを構築するというような意味を含んでいます。

教育学者は、この陶冶を二つに分類します。

生活に必要な、実質的な知識や技能の取得を重視する「実質陶冶」と、それに対しての知識を使いこなす力を発展させ、思考力や精神的能力を育てる「形式陶冶」です。

形式陶冶は、ただ知識を伝達するのではなく、実質的な側面を育もう、というのが狙いです。

この連載は、子どもたちへの数学的な形式陶冶を目指してきました。子どもたちの数学的な思考力を育て、将来、得た知識を楽しみながら使いこなせるように、その土台作りを親子で一緒に行って欲しい。そして、美しい陶器を作り上げるように、その力や考え方、味わい方を慈しみながら、大切に育んでいって欲しい、というメッセージを込めています。

少しでもお役に立てたならば幸いです。

（取材・文／志田実恵）