数学的思考力を未就学児のうちにつけさせるにあたって、周囲の大人がキャッチしたい、子どもの【動き】とフィードバック、その後アプローチの仕方を毎回3ステップでお伝えします。

子どもが物事の共通点である【同じ】を発見し、その【理由】探しができることをねらいとしています。

6回目は図形美の【理由】の気づきです。

今回は、図形の感覚を学びます。図形（関係）の感覚は、図形の関係概念でもあります。

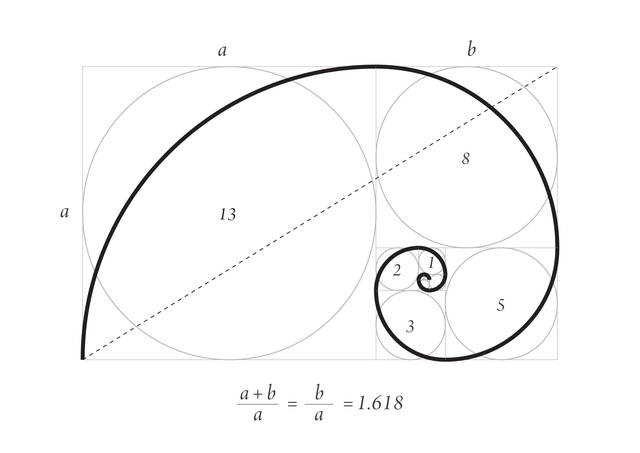
この形や配置は「どうしてきれいなのかな？」という疑問を出発点とし、「きれい」にかくれているひみつの「きまり」を探ります。

幼い子どもが「このおうちステキ！」と言ったり、車や電車を見て「かっこいい！」と喜んだりすることがありますよね。同じ種類の形同士を無意識にくらべっこしていた結果ではないでしょうか。

よく聞くと「パパ、京浜東北線より新幹線の方がかっこいい！」と主張することもあるでしょう。

美しさにも色々ありますが、数学美は図形と位置によるものです。

この数学美による「かっこよさ」の中には「形」と「位置」各々のバランスの良さという理由が隠れているのです。

1）形そのものがかっこいい

2）位置（レイアウト）＝置き方がかっこいい

形の位置、構成の位置、空間の中の位置が良い、ということもあるでしょう。

形と位置に共通していえる、バランスの美しさは、左右が同じという対象性のあるもの、線対象、点対象にあるものにも感じられます。

加えて、数学的には数量が加わる美しさもあります。丸が3個ある、四角が4個並んでいるというようなものです。

粘土遊びや、お絵かきをしている時、ブロックやパズルを敷き詰める時、おやつを並べる時にもこの「かっこよさ」は発見できそうですね。

基本的な、図形と図形の関係、さらに垂直や並行など、図形の中の関係を存分に味わってほしいですね。

図形と図形、つまり図形同士の関係は、変換と対称があります。

●合同変換：すべて同じ
●相似変換：合同から様々な要素を外したもの
●位相変換：同じ要素がものがすごく少ない（トポロジー）

一番レベルの高い変換は合同変換です。全て同じだからです。

子どもは結構こういうのが自然にできます。ドーナツとコーヒーカップが同じに見えるでしょうか？幼い子どもでも「こことここが同じだから、ドーナツもコーヒーカップも同じ！」と発見できそうですね。

このドーナツとコーヒーカップ、例えば円と正方形であっても、「閉じられている」という点では同じ「位相変換」なのです。

また、図形の中の関係（構成要素の関係）には、垂直や並行があります。これも存分に味わってほしいですね。

20世紀後半に発見された美しさが「フラクタル」です。コンピューターの発達により、容易にでききるようになったもので、簡単にいうと【部分と全体が同じ。部分が全体になっている】のです。フラクタルによって線、そして地図が数式で描けるようになったのです。

日本語でいうと自己相似性です。蔦などの植物、野菜などにも見られる「相似変換」です。

点から線、面、立体への「変換」をしながら違いに触れていきましょう。

立体の中に平面を見つけるのもいいですね。2次元から3次元をイメージする、影絵遊びなんかも良いと思います。

代表的なのは折り紙です。一枚の正方形の紙で、いろいろな幾何図形を作れ、立体に変わります。

そして、今までのSTEPの要素が全部入っています。折ったら「合同」があります。端と端をくっつけて折るのは「対応」の概念です。折り紙が数学になっていることはご存知ですか？日本発で、折り紙で数理学・幾何学を学ぶユニークな科学「オリガミクス」の世界です。

日本はこれを未就学児のうちに学べるのだから素晴らしいですよね。

「シェマ」という言葉があります。概念や認識の枠組み、モノの見方と訳されたり、表現されたりすることが多いですが、私はシェマを、多くの人の間で”わかるわかる”と共通理解できる形やイメージじゃないかと考えています。

つまり、シェマは一つの言語のようなものです。 絵文字にも近く、何らかの情報や注意を示す視覚記号に「ピクトグラム」がありますが、これも、シェマに近い表現形式かもしれないですね。

似たような状態を表すものに、心理学用語で「メンタルモデル」があります。同様に物事に対して持っているイメージのことを指しますが、もっとパーソナルなものです。

親子はこのメンタルモデルを幼い頃から容易に共有しやすいようですね。家庭で、メンタルモデルを育てた後、幼稚園や保育園などの社会活動を通じてシェマになっていくのではないでしょうか。その「シェマ形成」する経験をしっかり増やした上で、学校にあがってから、言語による「概念」を形成するとちゃんと身につくのだと思います。

だから、この「シェマ形成」の部分をとても大事にしてほしいと思っています。

図形は一つの共通言語にもなっています。だから、やっぱりこの【図形の共通認識】を幼少期のうちに意識して、育てておいてほしいですね。

次回第7回目は、”子どもが「生活にあるものやこと」はすべて変わっていくもの。しかも、変われば変わる関係だ”という気づきが「多変数」に繋がること、関数の考え方の一歩まで、一緒に紐解いていきます。

（取材・文/志田実恵）